Calculo Integral: 4.1 Definicion de Serie

miércoles, 1 de junio de 2011

4.1 Definicion de Serie

4.1.1Serie finita

x i = 0

para todo

i > n

y i = 0

para todo

i > m

. En este caso el producto de Cauchy de $\sum x_i$ y $\sum y_i$ se verifica es $(x_0+\cdots + x_n)(y_0+\dots+y_m)$ . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.

4.1.2Serie infinita

Primer ejemplo. Para alguna $a,b\in\mathbb{R}$ , sea $x_n = a^n/n!\,$ y $y_n = b^n/n!\,$ . Entonces

$C(x,y)(n) = \sum_{i=0}^n\frac{a^i}{i!}\frac{b^{n-i}}{(n-i)!} = \frac{(a+b)^n}{n!}$

por definición y la fórmula binomial. Dado que, formalmente, 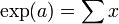$\exp(a) = \sum x$ y $\exp(b) = \sum y$ , se ha demostrado que $\exp(a+b) = \sum C(x,y)$ . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula

exp(a + b) = exp(a)exp(b)

para todo $a,b\in\mathbb{R}$ .

Segundo ejemplo. Sea $x (n) = 1$ para todo $n\in\mathbb{N}$ . Entonces $C (x, x)(n) = n + 1$ para todo $n\in\mathbb{N}$ por lo tanto el producto de Cauchy $\sum C(x,x) = (1,1+2,1+2+3,1+2+3+4,\dots)$ y no es convergente.

2 comentarios:

DOROTEO HERNANDEZ6 de diciembre de 2011, 0:50
que es eso
ResponderEliminar
Respuestas
Itzii3416 de mayo de 2012, 12:34
No se le entiende muy bien no solo por la explicación sino por las letras que usan con imágenes en negro con fondo negro, chequeen eso
ResponderEliminar
Respuestas

Añadir comentario